More on debt

Following my last post on debt I've thought a bit more, and received some very useful emails from colleagues. 

A central clarifying thought emerges. 

The main worry I have about US debt is the possibility of a debt crisis. I outlined that in my last post, and (thanks again to correspondents) I'll try to draw out the scenario later. The event combines difficulty in rolling over debt, the lack of fiscal space to borrow massively in the next crisis. The bedrock and firehouse of the financial system evaporates when it's needed most. 

To the issue of a debt crisis, the whole debate about r<g, dynamic inefficiency, sustainability, transversality conditions and so forth is largely irrelevant. 

We agree that there is some upper limit on the debt to GDP ratio, and that a rollover crisis becomes more likely the larger the debt to GDP ratio.  Given that fact, over the next 20-30 years and more, the size of debt to GDP and the likelihood of a debt crisis is going to be far more influenced by fiscal policy than by r-g dynamics. 

In equations with D = debt, Y = GDP, r = rate of return on government debt, s = primary surplus, we have* \[\frac{d}{dt}\frac{D}{Y} = (r-g)\frac{D}{Y} - \frac{s}{Y}.\] In words, growth in the debt to GDP ratio equals the difference between rate of return and GDP growth rate, less the ratio of primary surplus (or deficit) to GDP. 

Now suppose, the standard number, r>g, say r-g = 1% or so. That means to keep long run average 100% debt/GDP ratio, the government must run a long run average primary surplus of 1% of GDP, or $200 billion dollars. The controversial promise r<g, say r-g = -1%, offers a delicious possibility: the government can keep the debt/GPD ratio at 100% forever, while still running a $200 billion a year primary deficit! 

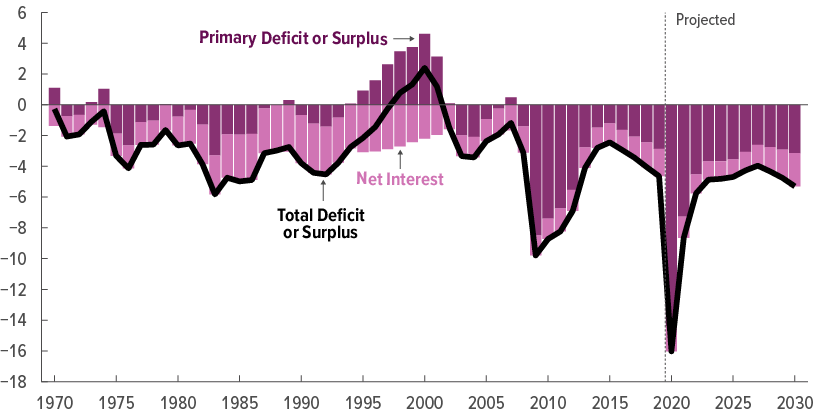
But this is couch change! Here are current deficits from the CBO September 2 budget update

We were running $1 trillion deficits before the pandemic. Each crisis seems to bring greater stimulus.  

I especially like this view because it doesn't make sense that an interest rate 0.1% above the growth rate vs. an interest rate 0.1% below the growth rate should make a dramatic difference to the economy. Once you recognize some limit on the debt/GDP ratio, and desirability of some long-run stable debt/GDP, there is no big difference between these two values. The surplus required to stabilize debt to GDP smoothly runs from negative couch change to positive couch change. 

I find this a liberating proposition. I find the whole sustainability, long run limits, dynamic inefficiency, transversality condition and so forth a big headache. For the question at hand it doesn't matter! (There are other questions for which it does matter, of course.) 

As we look forward,  debt/GDP dynamics for the next 20 years are going to be dominated by the primary surplus/deficit, not plausible variation in r-g. The CBO's 10 years of 6-8% of GDP overwhelm 1-2% of r-g. If each crisis continues to ratchet up 10% of GDP deficits per year, more so. The Green New Deal, and large federal assumption of student debts, state and local debts, pension obligations, and so forth would add far more to debt/GDP than decades of r vs. g.  

**********

Now that this is clear, I realize I did not emphasize enough that Olivier Blanchard's AEA Presidential Address  acknowledges well the possibility of a debt crisis: 

Fourth, I discuss a number of arguments against high public debt, and in particular the existence of multiple equilibria where investors believe debt to be risky and, by requiring a risk premium, increase the fiscal burden and make debt effectively more risky. This is a very relevant argument, but it does not have straightforward implications for the appropriate level of debt.

See more on p. 1226. Blanchard's concise summary

there can be multiple equilibria: a good equilibrium where investors believe that debt is safe and the interest rate is low and a bad equilibrium where investors believe that debt is risky and the spread they require on debt increases interest payments to the point that debt becomes effectively risky, leading the worries of investors to become self-fulfilling.

Let me put this observation in simpler terms. Let's grow the debt / GDP ratio to 200%, $40 trillion relative to today's GDP. If interest rates are 1%, then debt service is $400 billion. But if investors get worried about the US commitment to repaying its debt without inflation, they might charge 5% interest as a risk premium. That's $2 trillion in debt service, 2/3 of all federal revenue. Borrowing even more to pay the interest on the outstanding debt may not work. So, 1% interest is sustainable, but fear of a crisis produces 5% interest that produces the crisis. 

Brian Riedi at the Manhattan Institute has an excellent exposition of debt fears. On this point, 

... there are reasons rates could rise. ...

market psychology is always a factor. A sudden, Greece-like debt spike—resulting from the normal budget baseline growth combined with a deep recession—could cause investors to see U.S. debt as a less stable asset, leading to a sell-off and an interest-rate spike. Additionally, rising interest rates would cause the national debt to further increase (due to higher interest costs), which could, in turn, push rates even higher.

***********

So how far can we go? When does the crisis come?  There is no firm debt/GDP limit. 

Countries can borrow a huge amount when they have a decent plan for paying it back. Countries have had debt crises at quite low debt/GDP ratios when they did not have a decent plan for paying it back. Debt crises come when bond holders want to get out before the other bond holders get out. If they see default, haircuts, default via taxation, or inflation on the horizon, they get out. r<g contributes a bit, but the size of perpetual surplus/deficit is, for the US, the larger issue. Again, r<g of 1% will not help if s/Y is 6%. Sound long-term financial strategy matters. 

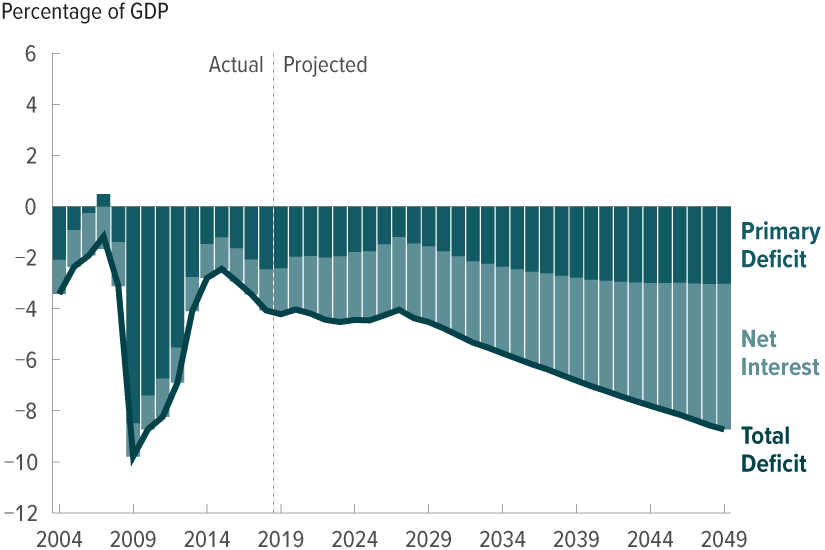
From the CBO's 2019 long term budget outlook (latest available) the outlook is not good. And that's before we add the new habit of massive spending. 

Here though, I admit to a big hole in my understanding, echoed in Blanchard and other's writing on the issue. Just how does a crisis happen? "Multiple equilibria" is not very encouraging. Historical analysis suggests that debt crises are sparked by economic and political crises in the shadow of large debts, not just sunspots.  We all need to understand this better.  

******

Policy. 

As Blanchard points out, small changes do not make much of a difference.  

 a limited decrease in debt—say, from 100 to 90 percent of GDP, a decrease that requires a strong and sustained fiscal consolidation—does not eliminate the bad equilibrium. ...

Now I disagree a bit. Borrowing 10% of GDP wasn't that hard! And the key to this comment is that a temporary consolidation does not help much. Lowering the permanent structural deficit 2% of GDP would make a big difference! But the general point is right. The debt/GDP ratio is only a poor indicator of the fiscal danger. 5% interest rate times 90% debt/GDP ratio is not much less debt service than 5% interest rate times 100% debt/GDP ratio. Confidence in the country's fiscal institutions going forward much more important. 

At this point the discussion usually devolves to "Reform entitlements" "No, you heartless stooge, raise taxes on the rich." I emphasize tax reform, more revenue at lower marginal rates. But let's move on to unusual policy answers. 

Borrow long. Debt crises typically involve trouble rolling over short-term debt. When, in addition to crisis borrowing, the government has to find $10 trillion new dollars just to pay off $10 trillion of maturing debt, the crisis comes to its head faster. 

As blog readers know, I've been pushing the idea for a long time that especially at today's absurdly low rates, the US government should lock in long-term financing. Then if rates go up either for economic reasons or a "risk premium" in a crisis, government finances are much less affected. I'm delighted to see that Blanchard agrees: 

to the extent that the US government can finance itself through inflation-indexed bonds, it can actually lock in a real rate of 1.1 percent over the next 30 years, a rate below even pessimistic forecasts of growth over the same period

It's not a total guarantee. A debt crisis can break out when the country needs to borrow new money, even absent a roll over problem. But avoiding the roll-over aspect would help a lot! Greece got in trouble because it could not roll over debts, not because it could not borrow for one year's spending. 

Contingent plans? Blanchard's concise summary adds another interesting option 

 contingent increases in primary surpluses when interest rates increase. 

I'm not quite sure how that works. Interest rates would increase in a crisis precisely because the government is out of its ability or willingness to tax people to pay off bondholders. Does this mean an explicit contingent spending rule? Social security benefits are cut if interest rates exceed 5%? That's an interesting concept. 

Or it could mean interest rate derivatives. The government can say to Wall Street (and via Wall Street to wealthy investors) "if interest rates exceed 5%, you send us a trillion dollars." That's a whole lot more pleasant than an ex-post wealth tax or default, though it accomplishes the same thing. Alas, Wall Street and wealthy bondholders have lately been bailed out by the Fed at the slightest sign of trouble so it's hard to say if such options would be paid. 

Growth. Really, the best option in my view is to work on the g part of r-g. Policies that raise economic growth over the next decades raise the Y in D/Y, lowering the debt to GDP ratio; they raise tax revenue at the same tax rates; and they lower expenditures. It's a trifecta. In my view, long-term growth comes from the supply side, deregulation, tax reform, etc. Why don't we do it? Because it's painful and upsets entrenched interests. For today's tour of logical possibilities if you think demand side stimulus raises long term growth, or if you think that infrastructure can be constructed without wasting it all on boondoggles, logically, those help to raise g as well. 

********

*Start with \(\frac{dD}{dt} = rD - s.\) Then \( \frac{d}{dt}\frac{D}{Y} =  \frac{1}{Y}\frac{dD}{dt}-\frac{D}{Y^2}\frac{dY}{dt}.\)

from The Grumpy Economist https://ift.tt/2DECiay